Что надо знать о дюрации и выпуклости облигаций

Каждому инвестиционному активу в той или иной степени присущи риски. Своя группа рисков характерна и для такого надёжного и консервативного инструмента, как облигация. В этой статье рассматривается одна из важнейших характеристик облигации – дюрация. Сегодня расскажу, что это такое и как использовать показатель дюрации облигаций.

Что такое дюрация простыми словами

Важно! Я веду этот блог уже почти 10 лет. Все это время я регулярно публикую отчеты о результатах публичных инвестиций. Сейчас мой публичный инвестпортфель - более 5 000 000 рублей.

Со временем этот сайт стал больше базой знаний для читателей, а все актуальные события в портфеле и не только я публикую в открытом телеграм-канале. Подписывайтесь, если хотите быть в курсе того, куда я инвестирую.

Подписаться

Рыночная цена и эффективная доходность облигации – величины непостоянные. Они меняются вместе с ситуацией на денежном рынке и особенно сильно зависят от ключевой ставки центрального банка. При значительном её повышении ранее выпущенные облигации вынуждены конкурировать с новыми выпусками, имеющими, как правило, уже более высокие купоны. Такая конкуренция приводит к тому, что инвесторы стремятся избавиться от менее доходных бумаг, а выравнивание доходностей достигается благодаря падению рыночных цен на облигации с меньшим купоном.

Например, с ростом ключевой ставки ЦБ на 2% годовых бумага с постоянным купоном должна подешеветь также на 2%, помноженные на оставшееся число лет обращения. Но выгоду от покупки такой облигации дешевле номинала инвестор получит только после погашения, тогда как более высокий купонный доход с другой бумаги он может получать сразу после приобретенияя. В условиях экономической неопределённости инвесторы из облигаций с равной доходностью предпочитают или более краткосрочные, или с большей ставкой купона.

В обоих случаях возврат вложенных денег наступает раньше. Величина, связывающая ставку купона со сроком погашения и текущей ценой облигации, называется дюрацией. В несколько упрощённом виде её можно представить как срок, за который инвестор возвращает вложенные средства. Поэтому дюрация измеряется в единицах времени. Например, в терминале QUIK она показана в днях. Дюрация бескупонной облигации совпадает со сроком до погашения.

Для купонных бумаг дюрация всегда меньше срока погашения, т. к. кроме возврата суммы номинала инвестор получает купонный доход. Например, если ставка купона 3-летней облигации равна 7%, общие выплаты составят 121% от номинала. Тогда срок возврата инвестиции (без учёта инфляции) будет равен 100/121*3*365=905 дней. В определённом смысле это абстракция, но покупая бумагу с такой дюрацией, инвестор рискует меньше, чем при погашении всей суммы в последний день, т. е., через 1095 дней.

Формула дюрации и что она означает

Математическую основу этой характеристики разработал Ф. Маколей, поэтому иногда говорят о дюрации Маколея.

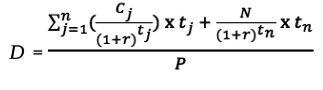
C – ставка купона;
Р – текущая рыночная цена;
N – номинал;
r – доходность к погашению;
n – число купонных выплат;
t – срок выплаты (купон или погашение).

В этой формуле отсутствует ставка дисконтирования, учитывающая инфляцию, но в неявном виде она уже заложена в рыночной цене облигации.

Расчёты кажутся сложными, но на практике заниматься ими инвестору не придётся: готовые значения дюрации он видит в торговом терминале.

Прежде всего, дюрация данной бумаги – это величина непостоянная. Она меняется вместе с доходностью. Может возникнуть вопрос: в чём же тогда практическая польза этого показателя? Для одной конкретной облигации он действительно несёт мало смысловой нагрузки. Но при сравнении текущей дюрации разных выпусков бумаг полезно ориентироваться на общие закономерности:

• Выше ставка купона – ниже дюрация;
• Больше дней до погашения – больше дюрация;
• Ниже доходность к погашению – больше дюрация;
• Больше дюрация – цена сильнее зависит от ключевой ставки ЦБ.

Это означает, что если прогнозируется повышение ключевой ставки, инвестору желательно перейти в бумаги с более низкой дюрацией: так его портфель будет застрахован от снижения доходности по сравнению с рынком. Для портфеля облигаций общая дюрация равна сумме произведений показателей каждой бумаги на её долю в портфеле. Например, для двух облигаций с дюрациями 1500 и 1700 и долями в портфеле соответственно 60% и 40%, общая дюрация будет равна 0,6*1500 + 0,4*1700 = 1580. Поддержание постоянной дюрации портфеля помогает сохранять равномерность денежного потока. По мере погашения выпусков и поступления купонных платежей, докупаются новые облигации с дюрацией, максимально близкой к данной характеристике портфеля.

Модифицированная дюрация

Можно сказать, что дюрация отражает степень риска данной бумаги или портфеля. Но такой подход слишком упрощён и не всегда удобен на практике, особенно при относительно краткосрочных покупках. Поэтому часто применяется т. н. модифицированная дюрация. На очень узком интервале изменения рыночной доходности модифицированная дюрация близка к процентному колебанию цены облигации с изменением доходности на 1%.

MD = D/(1+Y/100);

ΔР=-MD*Δy, где

MD – модифицированная дюрация;
D – дюрация (в годах или днях);
Y – эффективная доходность бумаги в %;
ΔР – изменение цены бумаги в %;
Δy – изменение доходности на рынке в %.

Знак «-» означает, что при росте доходности цена облигации падает, и наоборот. Если показатель измеряется в днях, то модифицированную дюрацию нужно дополнительно разделить на 365. Пусть, например, облигация торгуется по 1050 руб., её дюрация равна 1000, а эффективная доходность 8%. Тогда модифицированная дюрация будет равняться 2,54. При увеличении рыночной доходности до 10%, стоимость бумаги должна упасть на 5,08%: 1050*((100-5,08)/100)=997 руб.

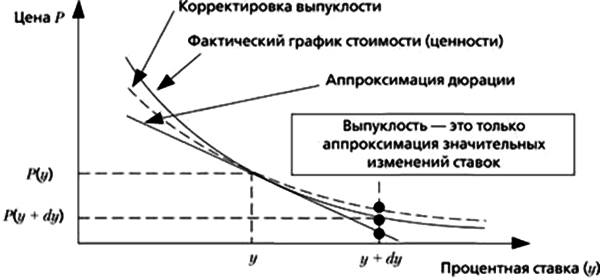
В общем случае график «цена облигации — доходность» представляет собой кривую. Чем сильнее меняется ключевая ставка, тем больше цена отклоняется от расчётных значений. При росте ставки стоимость облигации обычно снижается меньше, чем растет при понижении ставки. Для понимания причины этого явления следует ввести ещё одну величину – выпуклость кривой цена-доходность облигации.

Выпуклость облигаций и как она влияет на цену

Формула, связывающая изменение стоимости бумаги с изменением доходности и с выпуклостью, имеет вид:

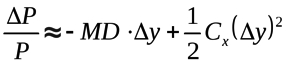
ΔР – изменение цены;
Δy – изменение доходности;
MD – модифицированная дюрация;
С_х – коэффициент выпуклости.

Эта формула приблизительная, и в ней не учтены поправки более сложного порядка, но они невелики и ими можно пренебречь. Для большинства непрофессиональных инвесторов знание выпуклости облигации необязательно, но оно помогает в случае неопределённости с политикой ставок ЦБ. При прочих равных условиях облигация с большей выпуклостью меньше зависит от рынка и поэтому предпочтительнее для портфельного инвестирования. С повышением ставки она медленнее дешевеет, а со снижением – быстрее дорожает.

На этом явлении (точнее, на аномальном отклонении от него) основана популярная стратегия – торговля спредами доходности. Теоретически облигации одного эмитента с близкими значениями дюрации и выпуклости должны иметь узкий спред доходности. Если же для отдельных выпусков спред оказывается резко расширенным, это явление обычно носит краткосрочный характер: рынок выравнивает доходности за счёт цены. Поэтому инвестор может получить прибыль от покупки облигации с аномально большой доходностью с последующей продажей по более высокой цене. Аналогично он может продать облигацию с аномально упавшей доходностью, выкупив её затем по более низкой цене. Знание дюрации и выпуклости в моменте как раз и позволяют оценить уровень риска подобных сделок. Рассчитать простую и модифицированную дюрацию, выпуклость и другие характеристики для конкретных выпусков можно с помощью калькулятора облигаций на сайте rusbonds.ru.

Выводы

Дюрация и выпуклость – это важные характеристики облигаций. На них основано множество торговых и инвестиционных стратегий. В короткой статье невозможно дать исчерпывающие рекомендации, но основные легко понять и запомнить:

• Из бумаг одного эмитента с похожими характеристиками предпочтительнее те, у которых ниже дюрация;
• Из облигаций одного эмитента с близкими значениями показателя меньший риск обеспечивают более выпуклые;
• Чем меньше различаются дюрации бумаг в портфеле, тем равномернее денежный поток.

Надеюсь, у меня получилось доступно объяснить.

Всем профита!

(3 оценок, среднее: 3,67 из 5)

Загрузка...