Портфельная теория Марковица — что, где, когда?
Даже далёкие от инвестирования люди знают, что нельзя вкладывать все деньги в какой-либо один актив, каким бы надёжным он ни казался сегодня. В случае валют, например, лучше часть капитала держать в рублях, часть в швейцарских франках и долларах. Чем больше число активов, тем выше диверсификация рисков инвестиционного портфеля.
Содержание:
Математика, или не зря мы в школе учились
Важно! Я веду этот блог уже почти 10 лет. Все это время я регулярно публикую отчеты о результатах публичных инвестиций. Сейчас мой публичный инвестпортфель - более 5 000 000 рублей.
Со временем этот сайт стал больше базой знаний для читателей, а все актуальные события в портфеле и не только я публикую в открытом телеграм-канале. Подписывайтесь, если хотите быть в курсе того, куда я инвестирую.
Подписаться На помощь инвестору приходит математика. Впервые законченную систему создания сбалансированного по доходности и риску портфеля инвестиционных инструментов создал Гарри Марковиц. За эту систему, названную в честь него, Марковиц получил Нобелевскую премию. До сих пор основные правила портфельной теории Марковица применяются банками, инвестиционными компаниями и хедж-фондами. В настоящее время существует немало компьютерных программ, помогающих автоматизировать процесс структурирования портфеля. Тем не менее, понимать базовые принципы этой методики полезно каждому инвестору.
Основная идея теории Марковица состоит в том, что доходность инструмента и величина риска связаны между собой. Иными словами, риск является функцией от разброса значений доходности за ряд временных интервалов.
Подбор инструментов для портфеля начинается с оценки математического ожидания доходности каждого инструмента за рассматриваемое время. Это есть среднее арифметическое от доходностей за каждый интервал, а стандартное отклонение от графика доходности – мера риска. Очевидно, что в общем случае, чем выше величина доходности, тем больше по абсолютной величине и разброс значений, а потому и риск. Поясним это на конкретном примере. Пусть доходность за интервал времени имеет следующие значения:
| Период | 1 | 2 | 3 | 4 | 5 |
| Доходность, % | 2 | 3 | 5 | -2 | 4 |
Среднее арифметическое равно (2+3+5-2+4)/5=2,4%
Это и есть ожидаемая доходность. Если инвестиционный портфель состоит из некоторого числа инструментов, то общая ожидаемая доходность портфеля рассчитывается как сумма произведений доходностей отдельных инструментов на их долю в портфеле:
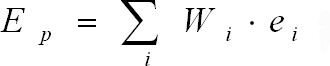
Ep – ожидаемая доходность портфеля;
ei – ожидаемая доходность i-го финансового инструмента;
wi-доля i-го финансового инструмента в портфеле.
Отклонение доходности инструмента от ожидаемой величины выражается через дисперсию:
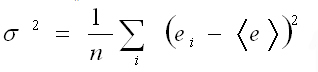
<e>– среднее значение инструмента за весь интервал;
n – количество периодов;
σ2 – дисперсия доходности инструмента на данном интервале.
Если воспользоваться значениями из таблицы выше, то получаем:
((2-2.4)2+(3-2.4)2+(5-2.4)2+(-2-2.4)2+(4-2.4)2)/5=29.2
Размерность дисперсии – процент в квадрате, что не очень удобно. Если извлечь из дисперсии квадратный корень, получим стандартное отклонение, что будет мерой риска. В данном случае, это 5.4%. Стандартное отклонение всего портфеля уже невозможно вычислить по такой же простой формуле, как это делалось с доходностью. Приходится вводить новую величину – ковариацию. Она показывает корреляцию между колебаниями величин, каждая из которых случайна. В нашем случае, это доходности рассматриваемых инструментов. Чтобы не усложнять, достаточно лишь упомянуть, что для формирования инвестиционного портфеля предпочтительнее использовать инструменты, колебания доходности которых находятся в разных фазах, т.е. не коррелируют.
Например, это могут быть акции нефтедобывающих и авиакомпаний. В случае падения нефтяных цен акции нефтедобывающих компаний неизбежно будут дешеветь, но в то же время будут дорожать акции авиакомпаний в связи со снижением себестоимости полётов.
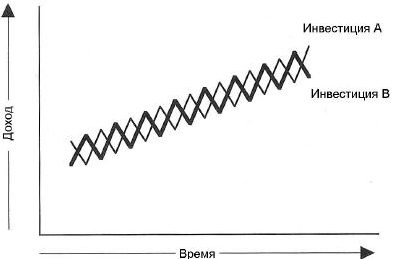
Портфель Марковица
Подход Марковица предполагает, что в портфеле не могут находиться короткие позиции по инструментам, т.е. спекулятивная составляющая в нём полностью отсутствует. Кроме того, доходность портфеля не может превышать максимальную из доходностей составляющих его инструментов. Грамотно составленный портфель должен быть сбалансирован с точки зрения доходности и риска таким образом, чтобы в идеале стремиться к непрерывному росту, хотя отдельные его составляющие могут временно терять в цене. Наиболее оптимальные комбинации инструментов образуют множество, называемые эффективными портфелями. Их ещё называют не улучшаемыми: для каждого из них невозможно добиться повышения доходности без одновременного повышения риска.
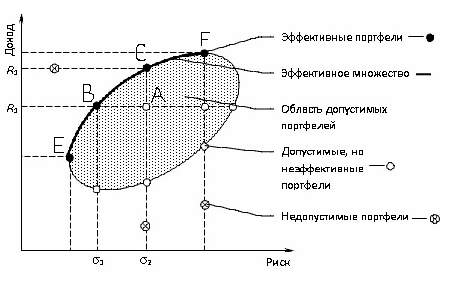
На этом графике кривая эффективных портфелей показывает максимально сбалансированные комбинации инструментов. Эту кривую отличает то, что приращение доходности больше, чем соответствующее ему приращение риска. Например, инструмент В имеет большую доходность по сравнению с инструментом Е, но и больший риск. В то же время, инструмент А при той же доходности, что и В, имеет ещё более высокое значение риска. Отсюда видно, что формирование портфеля на основе инструментов Е и В предпочтительнее, чем, например, Е и А или В и А. Кривая допустимых, но неэффективных портфелей отличается от кривой эффективных портфелей тем, что приращение риска, наоборот, больше приращения доходности. Тем не менее, и такие портфели можно рассматривать в качестве вариантов. Все портфели, находящиеся между указанными кривыми, попадают в множество допустимых портфелей. За пределами этого множества оказываются все остальные комбинации, образующие множество недопустимых портфелей. Они исключаются из рассмотрения.
Давайте теперь посмотрим, как можно пользоваться портфельной теорией Марковица на практике. В качестве примера можно взять сервис подбора портфеля на сайте «Сбербанк CIB» (sberbank-cib.ru/products/gm/it/instruments/optimal_portfolio.wbp). Это закрытое акционерное общество, созданное после покупки «Сбербанком» инвестиционной компании «Тройка Диалог». Вначале нужно выбрать ценные бумаги:
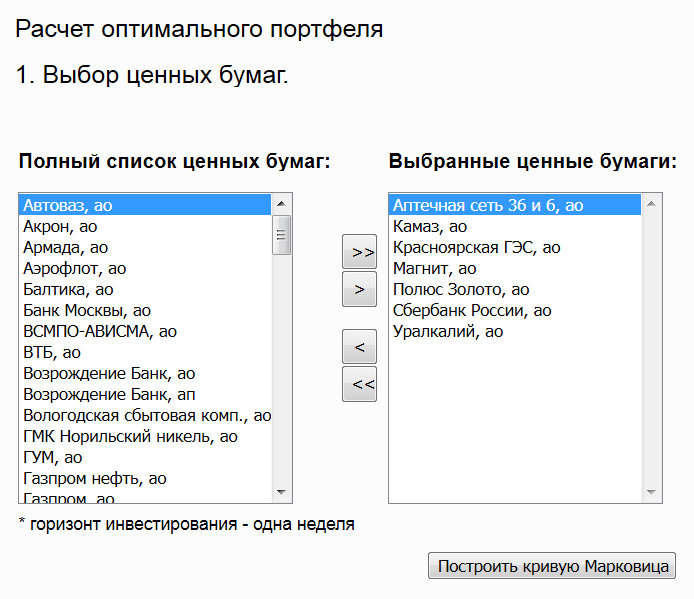
При нажатии на кнопку «Построить кривую Марковица» получаем график риск-доходность:
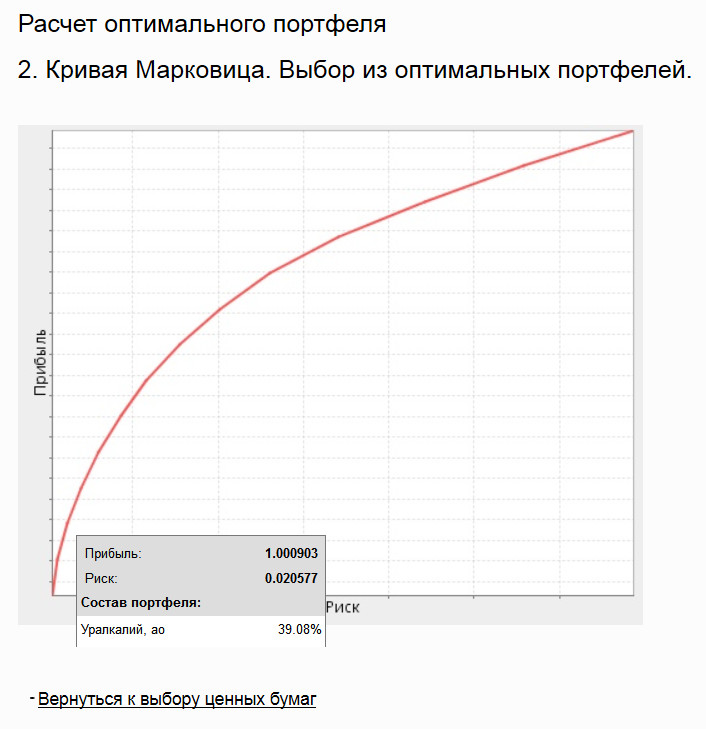
В данном случае кривая эффективных портфелей получается при доле бумаг АО «Уралкалий» в портфеле, равной 39,08%.
Слабые места теории Марковица
При растущем рынке теория Марковица в целом упрощает задачу инвестора. Проблемы появляются при развороте рынка. Основной принцип пассивной стратегии управления капиталом «купить и держать» на медвежьем рынке оборачивается нарастанием убытков. Математическое ожидание доходности зависит от выбранного интервала времени. Чем этот интервал больше, тем медленнее реагирует математическое ожидание на новый ряд значений. В целом, проблема во многом подобна использованию скользящих средних с очень длительным периодом.
Теория Марковица не содержит инструментария для определения точек входа и выхода из сделки. В связи с этим приходится всё чаще пересчитывать портфель, постепенно исключая из него лидеров падения. Запрет на короткие сделки означает, что на падающем рынке само понятие эффективного портфеля может терять смысл. Ещё одна проблема связана с тем, что поведение инструмента в прошлом не гарантирует повторения такого поведения в будущем. В настоящее время более популярны активные или комбинированные пассивно-активные стратегии, в которых портфельная теория сочетается с применением технического анализа для более оперативного реагирования на изменения рынка.
Выводы
Любая теория приносит пользу тем практикам, которые чётко осознают особенности её применения. Сильные и слабые стороны портфельной теории Марковица можно сформулировать следующим образом.
Сильные стороны:
- математический аппарат, позволяющий автоматизировать процесс формирования инвестиционного портфеля;
- возможность наглядного представления информации.
Слабые стороны:
- нет критериев входа и выхода из инструмента;
- теория мало пригодна при общем падении рынка;
- базируется на предыстории, но не использует методы прогноза.
Несмотря на то, что в настоящее время теория и практика инвестирования обогатились серьёзными научными методами анализа, портфельная теория Марковица по-прежнему широко используется, как важная часть математического инструментария. Надеюсь, у меня получилось простыми словами объяснить суть теории Марковица, которая не такая уж и сложная, как может показаться начинающему инвестору.
Всем профита!
(7 оценок, среднее: 5,00 из 5)
Загрузка...
- Где взять денег для инвестиций и на форекс
3 433 25 - Что такое IPO на биржевых рынках4 165 2
- Что нужно знать про наследование инвестиций4 740 8
- Что нужно знать про инвестиционные риски4 004 0
- Развивающиеся рынки: что нужно знать о них инвестору4 110 0
- Как защититься от утечки персональных данных2 532 0
- Кто такой миноритарный акционер и что даёт этот статус3 051 0
- Почему маржа прибыли Net Profit Margin так важна2 727 0
Кладбищенский бизнес или инвестиции в загробную жизнь
Подпишитесь на VK-сообщество Ленивых инвесторов, там говорим о самых актуальных новостях и делимся книгами.
Статья конечно «так себе».
1) Ковариация и корреляция — это разные вещи, в статье различия не улавливается, лучше говорить только о корреляции.
2) Ни слова про ребалансировку, важнейший этап для сохранения общего риска портфеля на одном уровне
3) «доходность портфеля не может превышать максимальную из доходностей составляющих его инструментов» — это не так, может
4) ну и применение теории к отдельным эмитентам — то еще извращение 🙂
1. По моему в статье я дал довольно точное определение ковариации
2. Статья обзорная, поэтому не ставил задачи объять все аспекты портфельной теории
3. Приведите пример.
4. Это был всего лишь пример)
1) Может быть и правда буквоедство. Есть же множество вариантов применения теории без вникания в суть, «готовых решений» масса.
2) Ребалансировка — момент КЛЮЧЕВОЙ. Правильное очень замечание, без него теория не имеет значения в диапазоне больше года.
3) Действительно. Вся суть портфельной теории Марковица, которая совершила микрореволюцию в момент опубликования САМОЙ первой статьи, сводится к целостности системы. Суммативный характер — сумма элементов, целостный — когда система ОТЛИЧАЕТСЯ от элементов своих. Так вот. Марковиц первым показал в расчетах и на практике, что портфельное распределение+ребалансировка=бОльший эффект.
Пример классический для рунета: портфель лежебоки Сергея Спирина.
4) Тоже соглашусь. Диверсификация по отраслям минимум (для Америки, Японии, Великобритании) и по видам активов для остального мира. Отдельные акции подгонять под портфельную теорию — сразу подписаться под убытками, к сожалению.
5) Я бы добавил еще один минус статьи. Если бы Марковиц был крайним в портфельной теории и непревзойденным, то после него Нобелевскую премию за аналогичные теории не выдавали)) Шутка))
Крупным минусом теории Марковица является неверный учет при формировании портфеля по его формулам активов с фиксированной доходностью. К примеру, в России 10% на вклад ОЧЕНЬ сильно меняет картину оптимального портфеля. Собственно, один из продолжателей теории Тобин в своих расчетах и своей модели это учел. Плюсы его теории — минусы Марковица;)
П.С.: отличная статья хотя бы потому, что в отличии от завсегдатаев комментаторов-новичков, данную статью комментируют знающие и разбирающиеся люди. Это достижение.
Не подскажите, где в сети можно про модель портфеля Тобина почитать, желательно на русском? Давно читал статейку на UT, не понравилась.
Если честно, вот так просто не скажу)) Пару лет назад плотно занимался, ничего стоящего не нашел. В итоге взял учебник, посчитал по формулам Тобина пару портфелей по России сам))
ПРИМЕРНО получилось то же, что и по Марковицу, примерно.
Но не для всех портфелей: при минимальном уровне риска на 10% Марковиц предлагал минимум акций и основу из недвижимости или золота. А вот Тобин где-то до 15% запаса прочности добавлял к портфелю Марковица долю вкладов (я считал по статистике ЦБ РФ с 1999 года). Для зарубежных рынков с отрицательной депозитной доходностью модель уже бессмысленная, может поэтому про неё слегка подзабыли))
К сожалению у вас сложилось в корне ошибочное мнение о современной портфельной теории. Слабые места теории и выводы описанные Вами почти не соответствуют самой теории, т.к. она расчитана на инвестирование, а не спекулирование.
Грань между инвестированием и спекулированием настолько тонка, что в большинстве случаев можно смело использовать первый термин
Огромное спасибо за статью!
Вот такие инвестиции, как результат работы мозга, мне очень нравятся 🙂
«для формирования инвестиционного портфеля предпочтительнее использовать инструменты, колебания доходности которых находятся в разных фазах (в таком случае говорят об отрицательной ковариации), т.е. не коррелируют.»
Вообще-то это 100% отрицательная корреляция. Если одна цена всегда понижается, когда повышается другая, то они по определению коррелируют.
Почему в графике эффективных портфелей точка на уровне доходности с точкой C является недопустимой? Ведь доходность по ней высокая, а уровень риска низкий?